FLUID DYNAMICS

FLUID DYNAMICS | REYNOLD'S EQUATION| NAVIER STOKES EQUATION| EULER'S EQUATION| ASSUMPTION| BERNOULLI'S EQUATION OF MOTION | ASSUMPTION OF BERNOULLI'S EQUATION | VENTURIMETER | ORIGICEMETER |PITOT TUBE | MOMENTUM EQUATION | KINETIC CORRECTION FACTOR | MOMENTUM CORRECTION FACTOR |

 FLUID DYNAMICS

Definition: - It is the branch of fluid mechanics which deals with the study of fluid in motion along with the force causing the flow. 

The force causing the flow of motion is determined by the Newton second law of motion.

According to Newton’s second law of motion –

F_x = m.a_x

When the flow of fluid is occurred in ‘x’ direction.

Where, F_x = Net force acting on fluid element in ‘x’ direction.

        a_x = acceleration of fluid element in ‘x’ direction.

In a fluid flow following forces are presents –

• F_g – Gravity force
• F_p – Pressure force
• F_v – Force due to viscosity
• F_t – Force due to turbulence
• F_c – force due to compressibility

 

Therefore F_x = (F_g)_x + (F_p)_x + (F_v)_x + (F_t)_x + (F_c)_x

 

If the force due to compressibility is neglected i.e. fluid is incompressible,

Then, F_x = (F_g)_x + (F_p)_x + (F_v)_x + (F_t)_x

-      This equation is called Reynold’s equation of motion.

 

If the force due to turbulence is neglected,

Then, F_x = (F_g)_x + (F_p)_x + (F_v)_x

-      This equation is called Navier-Stokes equation of motion.

 

If the force due to viscocity is neglected i.e. fluid is inviscid,

Then, F_x = (F_g)_x + (F_p)_x

-      This equation is called Euler’s equation of motion.

 

Euler’s Equation of motion: -

In Euler’s equation of motion only gravity force and pressure force is taken into consideration.

 

The differential form of Euler’s law of motion is-

dp/ρ + g.dx + v.dv = 0

Assumption: -

• The flowing fluid is incompressible.
• The flow of fluid is continuous, steady and along the streamline.
• The fluid is non-viscous.

 

Bernoulli’s Equation of motion: -

Bernoulli’s equation of motion is obtained by integrating Euler’s equation –

∫ dp/ρ + ∫ g.dx + ∫ v.dv = ∫ 0

As the flow is incompressible, ρ = cost.

P/ρ + g.z + v²/2 = const.

Or, P/ρg + v²/2g + z = const.

 

Assumption: -

• Fluid is ideal
• The fluid flow is steady
• The flow of fluid is incompressible
• The flow is irrotational

 

If Bernoulli’s equation is applied in two section of a pipe, then-

 

 P₁/ρg + v₁²/2g + z₁ = P₂/ρg + v₂²/2g + z₂

 

Where, z = Potential energy per unit weight or potential head

        v₁²/2g = Kinetic energy per unit weight or Kinetic head

        P/ρg = Work req. to maintain the flow per unit weight.

 

Bernoulli’s Equation for real fluid: -

P₁/ρg + v₁²/2g + z₁ = P₂/ρg + v₂²/2g + z₂ +h_l

Where h_l = head loss during flow.

 

Application of Bernoulli’s Equation: -

1.   Venturimeter, 2. Orificemeter, 3. Pitot tube.

 

Venturimeter: -

It is a device used for measuring the rate of flow flowing through a pipe.

Principle- Bernoulli’s Equation.

It consists of three parts-

Short converging portion

Throat

Diverging part

Expression for rate of flow through venturimeter-

Fig.1 | Venturimeter

Discharge 

Q_Th = [a₁a₂/ √(a₁² – a₂²)] √(2gh)          (Theoretical discharge)

Q_Act = c_d[a₁a₂/ √(a₁² – a₂²)] √(2gh)    (Actual discharge)

 

Where c_d = Coefficient of discharge for venturimeter

• The value of c_d is always less than 1.
• The length of diverging portion is three to four times larger than converging portion.
• Semi-angle of converging section is 18^o - 20^o
• Semi-angle of diverging section is less than 7^o
• Velocity of liquid is higher and pressure is lower in throat than inlet portion

 

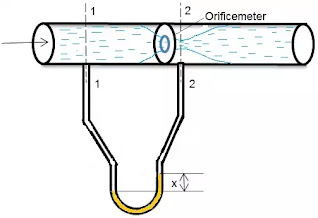
Orificemeter: -

• It is a device used for measuring the rate of flow flowing through a pipe.
• It is cheaper than venturimeter.
• It consists of a flat circular plate which has a circular sharp edged hole called orifice.
• Orifice is co-centric with the pipe.
• Diameter of orifice is generally 0.5 (vary 0.4-0.8) times of pipe diameter.

Discharge:

Fig.2 | Orificemeter

Q = c_d[a₀a₁/ √(a₁² – a₀²)] √(2gh)        (Actual discharge)

Where a₀ = Cross section area of orifice

        a₁ = area of pipe at section 1.

        a₂ = Cross section of vena contracta

 

Co-efficient of contraction C_c = a₂ / a₀

                  a₂ = C_c .a₀

 

 

Pitot tube: -

• It is a device used for measuring the velocity of flow at any point in a pipe or a channel.

Fig.3 | Pitot tube

Velocity at any point (v) = √(2gh)

• Velocity of ship and airplane is measured by pitot tube.

 

Momentum Equation: -Net force acting on a fluid or liquid is equal to the change in momentum per second in that direction.

 

From Newton’s second law –

F = ma

F = m.(dv/dt)

F = d(mv)/dt        - Momentum Equation

F.dt = d(mv)        - Impulse momentum Equation

 

Force exerted by a flowing fluid on a pipe bend: -

Fig. 4 | Bend pipe

F_x = ρQ (v₁ – v₂cosθ) + P₁A₁ – P₂A₂cosθ

F_y = ρQ (– v₂sinθ) – P₂A₂sinθ

 

F_R = √(F_x² + F_y²)

tanθ = F_y/F_x

 

Kinetic correction factor (α): -

α = (Kinetic energy per sec. based on actual velocity) / (Kinetic energy per sec. based on average velocity)

 

α = 1, for uniform velocity distribution

α = 1.022 – 1.15, for general turbulent flow

α = 2, for laminar flow

 

Momentum correction factor (β): -

β = (Momentum per sec. based on actual velocity) / (Momentum per sec. based on average velocity)

 

β = 1, for uniform flow

β = 1.01 – 1.07, for general turbulent flow

β = 1.33, for laminar flow in circular pipe with parabolic distribution

 

 

[Note – For details of calculation visit R.K. Bansal or any other book of Fluid Mechanics]